运筹学复习笔记

几种产品，利润最大的线性规划数学模型

解题方法

  1. 设第一样有x1x_1，第二样有x2...x_2...
  2. 确定目标函数maxz=c1x1+c2x2+...+cnxnmax z= c_1x_1 + c_2x_2 + ... + c_nx_n 或 minz=c1x1+c2x2+...+cnxnmin z= c_1x_1 + c_2x_2 + ... + c_nx_n
  3. 列个 s.t.{s.t.\lbrace 把各个约束条件列上去
  4. 在{\lbrace 最后写上 {\lbrace内各未知条件的取值范围

例题

某厂生产A、B、C三种产品，都需要用到煤、金属材料、电力资
源。各产品的单位产品利润、资源消耗以及现有生产资源如下：
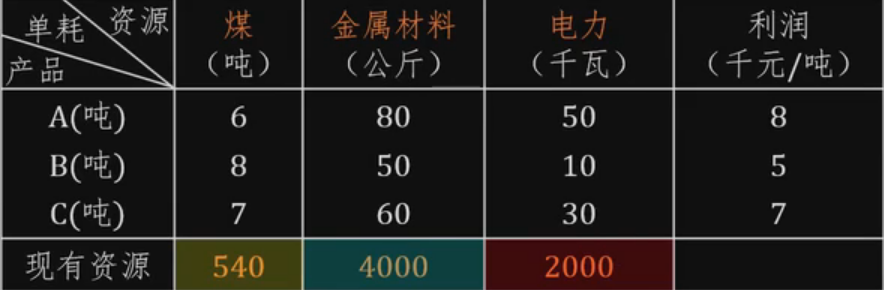
image.png
问如何制定生产计划可使该厂利润最大，请建立线性规划数学模型。

解题步骤

  1. 设A产品的产量是x1x_1吨，设B产品的产量是x2x_2吨，设C产品的产量是x3x_3吨。⇒\Rightarrow 煤共用了6x1+8x2+7x36x_1+8x_2+7x_3,金属共用了80x1+50x2+60x380x_1+50x_2+60x_3,电共用了50x1+10x2+30x350x_1+10x_2+30x_3,共赚了利润8x1+5x2+7x38x_1+5x_2+7x_3。
  2. maxz=8x1+5x2+7x3maxz = 8x_1+5x_2+7x_3
  3. s.t.{6x1+8x2+7x3≤54080x1+50x2+60x3≤400050x1+10x2+30x3≤2000x1,x2,x3≥0s.t.\begin{cases} 6x_1+8x_2+7x_3\leq540 \\ 80x_1+50x_2+60x_3 \leq 4000 \\ 50x_1+10x_2+30x_3 \leq 2000 \\ x_1,x_2,x_3 \geq 0 \end{cases}

化标准型

标准型目标：

  1. 目标函数为max的形式
  2. 多变量的式子都是等式
  3. 右侧的数字都是≥0\geq0的
  4. 式子中的变量都是≥0\geq0的

解题方法

  1. 将minα=amin \alpha=a变成maxβ=−amax\beta=-a
  2. 将大括号中多变量的式子都变成等式（给不等式加上或减去某个≥0\geq0的xnx_n,就能变成等式）
  3. 使所有式子最右边的数都≥0\geq0
  4. 将大括号中单变量的式子都变成啥≥0\geq0的形式，若某变量xm≤0x_m\leq0，则设置一个≥0\geq0的新变量xm′x_m^\prime,使xm′=−xmx_m^\prime=-x_m,这样可以将xm≤0x_m\leq0变成xm′≥0x_m^\prime\geq0。
  5. 若某变量xpx_p没提到\是自由变量\是无约束变量，这说明xpx_p可正可负可为0，则两个≥0\geq0的新变量xp′x_p^\prime、xp′′x_p^{\prime\prime}使xp′−xp′′=xpx_p^\prime - x_p^{\prime\prime}=x_p(因为两个≥0\geq0的数相减，结果就是可正可负可为0)
  6. 把大括号里所以单变量的式子，写到最下面一行。

例题

minz=3x1−x2+2x3minz=3x_1-x_2+2x_3
s.t.{2x1+x2−4x3≤1x1+2x2+2x3≥2x1+x2=−2x2≥,x3≤0s.t.\begin{cases} 2x_1+x_2-4x_3\leq 1 \\ x_1+2x_2+2x_3 \geq 2 \\ x_1+x_2 = -2 \\ x_2 \geq , x_3 \leq 0 \end{cases}

解题步骤

  1. maxβ=−3x1+x2−2x3max\beta = -3x_1+x_2-2x_3
  2. s.t.{2x1+x2−4x3+x4=1   x4≥0x1+2x2+2x3−x5=2   x5≥0x1+x2=−2x2≥,x3≤0s.t.\begin{cases} 2x_1+x_2-4x_3 + x_4 = 1 ~~~ x_4\geq0 \\ x_1+2x_2+2x_3 -x_5 = 2 ~~~ x_5\geq0 \\ x_1+x_2 = -2 \\ x_2 \geq , x_3 \leq 0 \end{cases}
  3. s.t.{2x1+x2−4x3+x4=1   x4≥0x1+2x2+2x3−x5=2   x5≥0−x1−x2=2x2≥,x3≤0s.t.\begin{cases} 2x_1+x_2-4x_3 + x_4 = 1 ~~~ x_4\geq0 \\ x_1+2x_2+2x_3 -x_5 = 2 ~~~ x_5\geq0 \\ -x_1-x_2 = 2 \\ x_2 \geq , x_3 \leq 0 \end{cases}
  4. s.t.{2x1+x2+4x3′+x4=1   x4≥0x1+2x2−2x3′−x5=2   x5≥0−x1−x2=2x2≥,x3′≥0s.t.\begin{cases} 2x_1+x_2+4x_3^\prime + x_4 = 1 ~~~ x_4\geq0 \\ x_1+2x_2-2x_3^\prime -x_5 = 2 ~~~ x_5\geq0 \\ -x_1-x_2 = 2 \\ x_2 \geq , x_3^\prime \geq 0 \end{cases}
  5. s.t.{2x1′−2x1′′+x2+4x3′+x4=1   x4≥0x1′−x1′′+2x2−2x3′−x5=2   x5≥0x1′′−x1′−x2=2x1′≥0,x1′′≥0,x2≥,x3′≥0s.t.\begin{cases} 2x_1^\prime- 2x_1^{\prime\prime} +x_2+4x_3^\prime + x_4 = 1 ~~~ x_4\geq0 \\ x_1^\prime- x_1^{\prime\prime}+2x_2-2x_3^\prime -x_5 = 2 ~~~ x_5\geq0 \\ x_1^{\prime\prime}- x_1^\prime-x_2 = 2 \\ x_1^\prime \geq0, x_1^{\prime\prime}\geq0 , x_2 \geq , x_3^\prime \geq 0 \end{cases}
  6. s.t.{2x1′−2x1′′+x2+4x3′+x4=1x1′−x1′′+2x2−2x3′−x5=2x1′′−x1′−x2=2x1′≥0,x1′′≥0,x2≥,x3′≥0,x4≥0,x5≥0s.t.\begin{cases} 2x_1^\prime- 2x_1^{\prime\prime} +x_2+4x_3^\prime + x_4 = 1 \\ x_1^\prime- x_1^{\prime\prime}+2x_2-2x_3^\prime -x_5 = 2 \\ x_1^{\prime\prime}- x_1^\prime-x_2 = 2 \\ x_1^\prime \geq0, x_1^{\prime\prime}\geq0 , x_2 \geq , x_3^\prime \geq 0 ,x_4\geq0 ,x_5\geq0\end{cases}

图解法

解题方法

  1. 画出x1Ox2x_1Ox_2坐标系，在坐标系中画出满足“{\begin{cases}\end{cases}”的区域MM。
    a.把“{\begin{cases}\end{cases}”内每个不等式都尽量变成x2x_2如何的式子
    b.讲不等式中的≥\geq,≤\leq变成==,得到几条直线并将这些直线画到x1Ox2x_1Ox_2坐标系中。
    c.若原不等式是{x2≥?,   画出直线上面的区域x2≤?,   画出直线下面的区域\begin{cases} x_2\geq?, ~~~ \text{画出直线上面的区域} \\ x_2\leq?, ~~~ \text{画出直线下面的区域} \end{cases}
    若原不等式是{x1≥?,   画出直线右面的区域x1≤?,   画出直线左面的区域\begin{cases} x_1\geq?, ~~~ \text{画出直线右面的区域} \\ x_1\leq?, ~~~ \text{画出直线左面的区域} \end{cases}
    d.各区域重合部分为MM
    若{区域M不存在,   则直接写答案，无解若区域M存在,   则继续步骤2\begin{cases} \text{区域M不存在}, ~~~ \text{则直接写答案，无解} \\ \text{若区域M存在}, ~~~ \text{则继续步骤2} \end{cases}

  2. 令目标函数左边等于0，得到直线LL,做出平行于直线LL,并且与MM相切的两条线，找出切点坐标，将坐标代入目标函数，求出值。

  3. 若要求maxmax，则得到最大值的切点为最优解；
    若要求minmin，则得到最肖值的切点为最优解；

注：若最优解是无数个点，则答：有无穷多解
若最优解在无穷远处，则答：解为无界解

运筹学复习笔记
https://www.zhaojun.inkhttps://www.zhaojun.ink/archives/36
作者
卑微幻想家
发布于
2021-03-16
许可协议